VAE的简要介绍

Part1从算法角度入手，以mnist数据集为例介绍VAE的输入输出，损失函数和基本理论，以及VAE的常见应用，附带Pytorch实现的VAE代码；Part2着重于概率论的理论分析，涉及到流形学习，稍微提到了与VAE相似的CAE。

原理

VAE对隐层输出增加长约束，在隐层采样过程中起到类似与dropout层的正则化作用，不容易过拟合。

由于VAE跟CAE的原理相似，以下补充CAE的简要介绍，可以跳过，不影响阅读。

CAE(constructive auto-encoder)
在auto-encoder上加入正则项，对权值进行惩罚：
$\mathcal{L}_{CAE}=\sum_{x\in D_n}(L(x,g(f(x)))+\lambda ||J_f(x)||^2_F)$
其中的正则项$Jf{x}$是隐层输出关于权值的雅可比矩阵，$||J{f}(x)||^2_{F}$是雅可比矩阵F范数的平方，即对雅可比矩阵中的每个元素求平方：
$||J_{f}(x)||^2_{F}=\sum_{ij}(\frac{\partial h_j(x)}{\partial x_i})^2\\=\sum_{i=1}^{d_h}(h_i(1-h_i))^2\sum_{j=1}^{d_x}W_{ij}^2$
CAE为什么在分类问题上表现好：
好的特征表示大致有2个衡量标准：1. 可以很好的重构出输入数据; 2.对输入数据一定程度下的扰动具有不变性。普通的autoencoder和sparse autoencoder主要是符合第一个标准，而deniose autoencoder和contractive autoencoder则主要体现在第二个。而对于分类任务来说，第二个标准更重要。雅克比矩阵包含数据在各种方向上的信息，Contractive autoencoder主要是抑制训练样本（处在低维流形曲面上）在所有方向上的扰动。
直接对auto-encoder的权值进行惩罚：
$\mathcal{L}_{AE+wd(\theta)}=\lgroup\sum_{x\in D_n}L(x,g(f(x)))\rgroup+\lambda\sum_{ij}W_{ij}^2$

对于高维数据而言，相似数据可能分布在高维空间的某个流形上，特征学习就是要显式或隐式地学习到这种流形。

以下补充流形学习的简要介绍，可以跳过，不影响阅读。

流形学习(Manifold Learning)
主要应用到数据降维与特征提取
思想：将高维数据映射到低维，使该低维数据能够反映高维数据的某些本质结构特征，即降维后仍能保持数据在高维中具有的某种结构特征。
流行学习的前提是一种假设：某些高维数据实际上是一种低维流形结构嵌入在高维空间中，而流行学习的目的是将其映射回低维空间中，揭示本质。通俗的讲，高维数据是由低维流形映射到高维空间上的，受限于数据内部特征，高维中数据会产生维度冗余，比如用二维直角坐标来描述一个圆是有冗余的，而使用极坐标来描述可以让这个描述方法所确定的所有点的集合都能在圆上，且只需要一个参数——半径。因此二维空间中的圆就是一个一维流形，与之类似的，三维空间中球面只需要用两个坐标(经纬度)来表示。
使用流行学习进行数据降维实际上是一种非线性降维，考虑距离和生成数据的拓扑结构。
由于流行学习可以刻画数据本质，因此深度学习中希望模型能够学习到数据在流行空间中的表示。什么样才是模型学习到了流行？模拟低维流形生成高维数据的生成过程，再通过对低维流行的微调，能够得到对应结构的高维数据(GAN)。GAN的生成过程即为输入一个特征空间的低维编码，得到一个输出空间的高维图像，由于流形空间是连续的，那么映射到高维空间的数据在流形连续调整时变得连续且有意义。

常见方法：局部改线嵌入(Local Linear Embedding, LLE)，拉普拉斯特征映射(Laplacian Eigenmaps, LE)，局部保持投影LPP，等距映射Isomap。

编码空间就是流形空间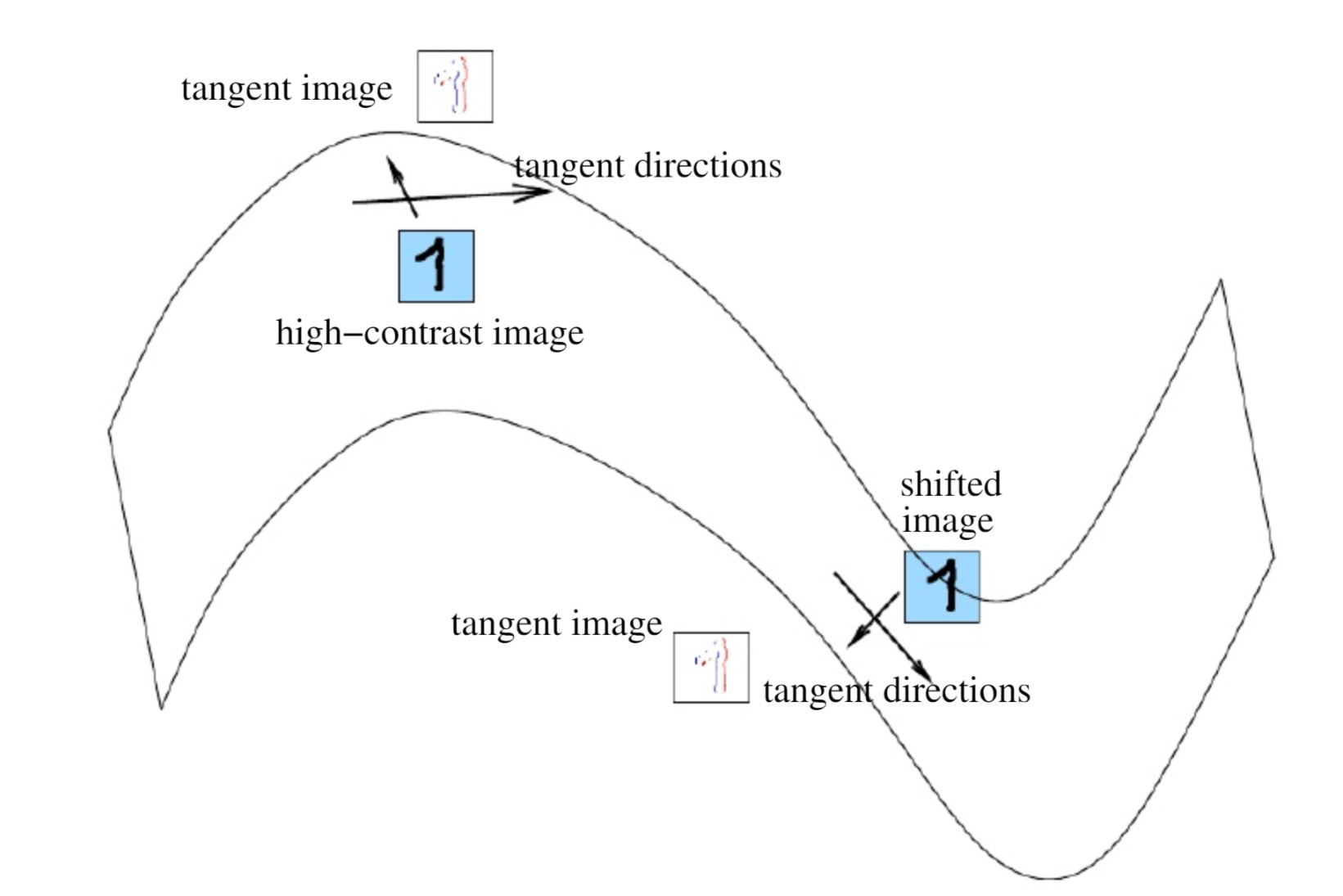
Alt text
从低维隐变量恢复高维观测变量。

问题陈述

观测变量$x$与隐变量$z$(latent variables)的关系如图：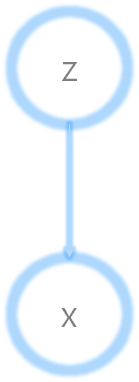
@观测变量与隐变量的关系

$x,z$都为向量，且观测变量的分布固定但未知。对于隐变量的先验概率$p(z)$，$x$相对于$z$的条件概率$p(x|z)$和隐变量的后验概率$p(z,x)$有如下关系：

$p(z,x)=p(x|z)p(z)$

$x$的边缘分布可以计算：

$p(x)=\int_zp(x,z)dz=\int_zp(x|z)\cdot p(z)dz=E_z[p(x|z)]$

而隐变量是不能被观测的，因此需要通过一个观察集$X$来估计概率图的相关参数。
如果一个机器学习模型可以显式或隐式地建模$p(z),p(x|z)$，这个模型就是生成模型，生成模型的含义是：

$p(z),p(x|z)$决定了联合分布$p(z,x)$
利用$p(z),p(x|z)$可以对$x$进行祖先采样：先按照概率生成采样点$z_i\sim p(z)$，再按照概率采样$x_i\sim p(x|z_i)$。

最简单的生成模型是朴素贝叶斯

以下补充对采样的简要介绍，可以跳过，不影响阅读。

sampling
what is sampling
已知一个随机变量$z$的分布$p(z)$，预个关于该变量的函数$f(z)$的值：$E_f=\int f(z)p(z)dz$
根据$p(z)$独立产生一系列采样点$z^{(l)}$，可以得到：
$\hat{f}=\frac{1}{L}\sum_{l=1}^Lf(z^{(l)})\rightarrow E_{\hat{f}}=E_f$
sampling methods
祖先采样法(ancestral sampling)
https://blog.csdn.net/hubin232/article/details/70171507
基本采样法(basic sampling)
拒绝采样法(reject sampling)
自适应拒绝采样法(adaptive reject sampling)
重要性采样法(importance sampling)

最大似然估计(Maximum Likelihood Estimation, MLE)

最大似然估计，就是利用已知样本结果，反推最有可能导致这样结果的参数值。最大似然中采样假设都是独立同分布。
一个直观解释

给定一组观测值$X=(x_i), i=1,\dots,n$，其似然为：

$L(p_\theta(X))=\prod_i^np_\theta(x_i)$

取对数：

$\log L(p_\theta(X))=\sum_i^n\log p_\theta(x_i)$

MLE假设最大化似然的参数$\theta^*$为最优参数估计，将参数估计问题转化为最大化$\log L(p_\theta(X))$问题。按照贝叶斯推理的观点，$\theta$本身作为随机变量服从某个分布$p(\theta)$:

$p(\theta|X)=\frac{p(\theta)\cdot (X|\theta)}{p(X)}=\frac{p(\theta)\cdot (X|\theta)}{\int_\theta p(X,\theta)d\theta}\propto p(\theta)\cdot (X|\theta)$

$\propto$表示正比
最大后验概率估计(MAP):

$\log p(\theta|X)=\log p(\theta)+\log L(p(X|\theta))$

期望最大化(Expectation-maximization, EM)

通过MLE得到了优化目标，其中存在对隐变量的积分，可以用EM算法解决。

EM解决了高斯混合模型(Gaussian Mixture Model, GMM)的参数估计和K-Means，语音识别中GMM-HMM模型的训练也用到了EM

MCMC

EM中涉及到对$p(z|x)$的积分，由于概率分布的多样性和变量高维，积分难以计算(intractable)。因此可以采用数值积分近似求M-step中的积分项，需要用MCMC按照$p(z|x)$对$z$进行采样

变分推理(Variation Induction)

由于MCMC过于复杂，在数据量大的情况下难以应用，需要使用其他近似解决方案。变分推理寻找一个易于处理的分布$q(z)$使其与$p(z|x)$尽可能接近，然后使用$q(z)$来代替。衡量分布间的相似程度使用KL散度，将寻找$q(z)$转换为优化问题：

$q^*(z)=argmax_{q(z)\in Q}KL(q(z)\|p(z|x))$

$KL(q(z)|p(z|x))$是关于$q(z)$的函数，$q(z)\in Q$也是一个函数，因此这是一个泛函(函数的函数)求极值。

变分求极值之于泛函，正如微分求极值之于函数

这是变分自编码器中变分(variation)的由来。

以下补充KL散度的简要介绍，可以跳过，建议阅读。

KL散度 (relative entropy)
$KL(P||Q)=\int_{-\infty}^{+\infty}p(x)\log\frac{p(x)}{q(x)}dx\\=\int_{-\infty}^{+\infty}p(x)\log p(x)dx-\int_{-\infty}^{+\infty}p(x)\log q(x)dx\\=H(P,Q)-H(P)\\=\text{cross entropy-entropy}$
$KL(P||Q)\neq KL(Q||P)$
$KL(P||Q)\geq 0, KL(P||Q)=0\text{ when }P=Q$

ELBO(Evidence Lower Bound Objective)

将最小化KL等价为最大化ELBO问题：

$KL(q(z)\|p(z|x))=\log p(x)-ELBO(q)$

$KL(q(z)\|p(z|x))=\int q\log \frac{q}{p}\\=E_q(\log q- \log p)\\=E_q[\log q(z)]-E_q[\log p(z|x)]\\=E_q[\log q(z)]-E_q[\log p(z,x)]+\log p(x)$

令$ELBO(q)=E_q[\log p(z,x)]-E_q[\log q(z)]$:

$\log p(x)=KL(q(z)\|p(z|x))+ELBO(q)\ge ELBO(q)$

因此ELBO是$p(x)$对数似然(evidence)的下限(lower bound)。

VAE

将ELBO记为$L$，通过优化$L$来优化$KL$。观测数据$x^{(i)}$的对数似然写为：

$\log p_{\theta}(x^{(i)})=KL(q_{\Phi}(z)\|p(z|x^{(i)}))+L(\theta, \Phi;x^{(i)})$

优化目标

$L(\theta, \Phi;x^{(i)})=E_{q_\Phi(z|x)}[\log p_{\theta}(x^{(i)}|z)]-KL(q_{\Phi}(z|x^{(i)})\|p_\theta(z))$

分解为优化$KL$和后验概率的对数似然：

$KL$优化：
$q$是要学习的分布，$p$是隐变量的先验分布，如果$q$取各维独立的高斯分布(Decoder)，令$p$为标准正态分布，可以计算出$KL$： $-KL(q_{\Phi}(z|x^{(i)})\|p_\theta(z))=-0.5*(1+\log\sigma_i^2-\mu_i^2-\sigma_i^2)\\=-0.5(1+\log\sigma^2-\mu^2-e^{\log\sigma^2})$
对数似然优化：这一项不能解析求出，考虑采样 $E_{q_\Phi(z|x)}[\log p_{\theta}(x^{(i)}|z)]\approx\frac{1}{L}\sum_{j=1}^L\log p_\theta(x^{(i)}|z^{(j)})$ 其中的$z^{(j)}$由reparameterization方法获得，如果每次只采一个样本点则有： $E_{q_\Phi(z|x)}[\log p_{\theta}(x^{(i)}|z)]\approx\log p_\theta(x^{(i)}|\tilde{z})$ 即为常用损失函数。

概率分布及对应损失函数

下面对encoder的损失函数推导对应的概率分布。
假设样本各维独立。

交叉熵
假设$p(x_i|z)$服从伯努利分布：$p(x=1|z)=\alpha_z,p(x=0)=1-\alpha_z$
对于某个观测值的似然为 $L=\alpha_z^x\cdot(1-\alpha_z)^{1-x}$ decoder的输出是伯努利分布的参数$\alpha_z=decoder(z)=\hat{x}$，得到对数似然： $\log L=x\cdot\log(\hat{x})+(1-x)\log(1-\hat{x})$ 取负即为交叉熵损失。
MSE
假设$p(x_i|z)$服从高斯分布：$p(x|z)=\frac{1}{\sqrt{2\pi}\sigma}\cdot e^{-\frac{(x-\mu)^2}{2\sigma^2}}$，对数似然为： $\log L=-0.5*\log(2\pi)-0.5*\log\sigma-\frac{(x-\mu)^2}{2\sigma^2}$ decoder是高斯分布的期望，方差$\sigma$为未知常数，优化目标为： $\max(-\frac{(x-\mu)^2}{2\sigma^2})=\min(x-\mu)^2$

指路Part1

Reference
VAE
manifold learning
CAE

VAE的简要介绍

Introduction to VAE(Variational Auto-Encoder) Part2

变分自编码器简介（二）