VAE的简要介绍
Part1从算法角度入手,以mnist数据集为例介绍VAE的输入输出,损失函数和基本理论,以及VAE的常见应用,附带Pytorch实现的VAE代码;Part2着重于概率论的理论分析,涉及到流形学习,稍微提到了与VAE相似的CAE。
输入输出
以mnist数据集为例,输入为m维,输出为n维的网络,称为decoder或者generative model,decoder结构可为MLP, CNN, RNN等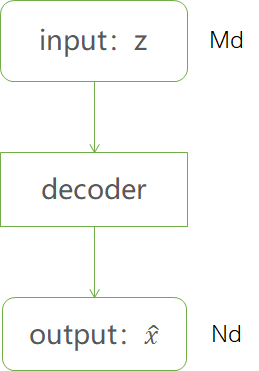
以mnist为例,6万张0~9手写灰度数字,大小28x28,将每个像素归一化到[0,1],训练集$X\subset[0,1]^{784}$,将输出也限定在此范围类,对decoder最后一层加入sigmoid激活。
训练
为了训练解码器,引入encoder(recognition model),输入为n维,输出为2*m维,也可以为任意合适的结构。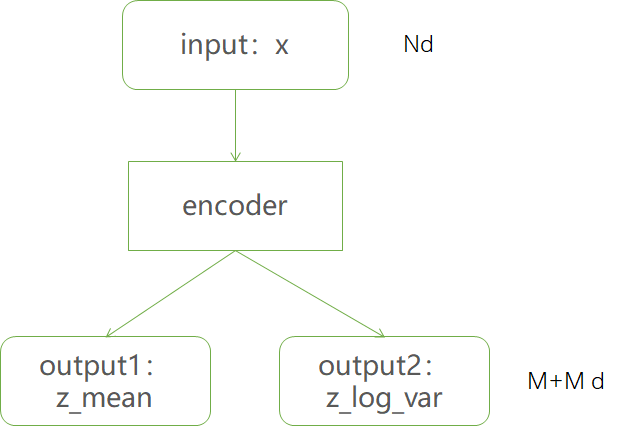
将encoder输出分别视为m个高斯分布的均值和方差的对数。然后根据输出的均值和方差生成服从相应高斯分布的随机数,作为decoder的输入,产生n维输出结果$\hat{x}$.
训练过程可以表示为: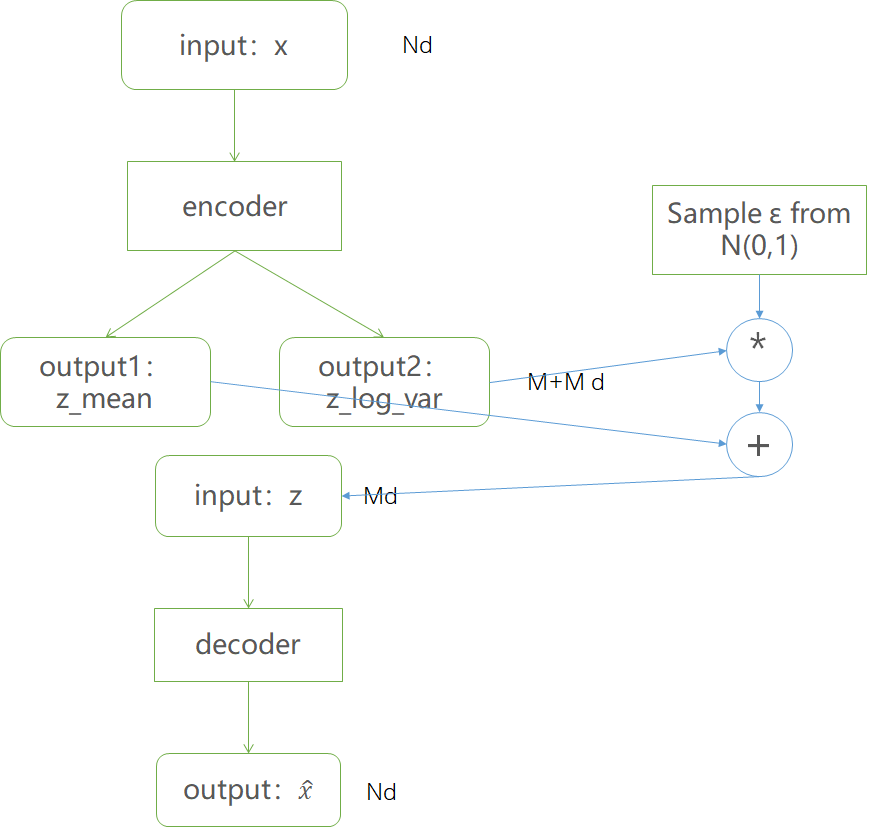
采样
reparameterize方法
由于$z\sim N(\mu,\sigma)$,应该从$N(\mu,\sigma)$采样,但这个采样操作对$\mu,\sigma$不可导,因此不能使用常规梯度下降进行反向传播。通过reparameterization,首先从$N(0,1)$分布中采样得到$\epsilon$,然后$z=\sigma\cdot\epsilon+\mu,z\sim N(\mu,\sigma)$.
这个从encoder的输出到decoder输入的过程只涉及线性操作,可以使用GD优化。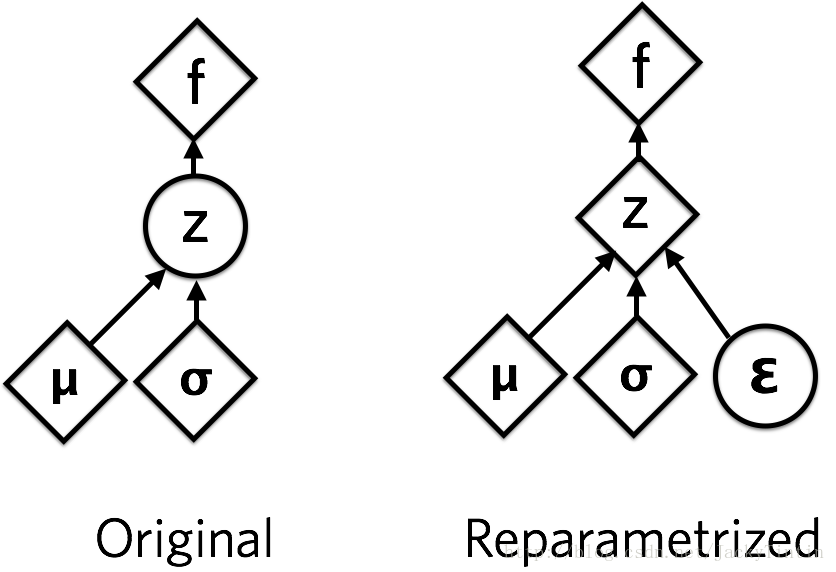
reparameterization的代价是隐变量连续。
损失函数
将encoder与decoder结合,对于训练集中的每个样本$x$都能输出相同维度的$
\hat{x}$结果,优化目标是使$x,\hat{x}$尽可能接近。使$x$经过编码后能够通过解码尽可能多的恢复出原有信息。
对于$x\in[0,1]$,使用交叉熵来衡量二者间的差异:
也可以用MSE损失函数:
训练过程中,输入就是输出,这是VAE中autoencoder自编码的含义
此外,需要对encoder输出的$\mu,\log\sigma^2$用KL散度加以约束:(为什么使用这一项为约束将在第二部分最后一节中进行分析)
所以最终的损失函数为:
或者:
训练过程中只使用了$x$的数据,既是输入也是gt,与其标签无关,因此是无监督学习。
code
VAE Pytorch Implementationclass Encoder(nn.Module):
def __init__(self, dims, sample_layer=GaussianSample):
super(Encoder, self).__init__()
[x_dim, h_dim, z_dim] = dims
neurons = [x_dim, *h_dim]
linear_layers = [nn.Linear(neurons[i-1], neurons[i]) for i in range(1, len(neurons))]
self.hidden = nn.ModuleList(linear_layers)
self.sample = sample_layer(h_dim[-1], z_dim)
def forward(self, x):
for layer in self.hidden:
x = F.relu(layer(x))
return self.sample(x)
class Decoder(nn.Module):
def __init__(self, dims):
super(Decoder, self).__init__()
[z_dim, h_dim, x_dim] = dims
neurons = [z_dim, *h_dim]
linear_layers = [nn.Linear(neurons[i-1], neurons[i]) for i in range(1, len(neurons))]
self.hidden = nn.ModuleList(linear_layers)
self.reconstruction = nn.Linear(h_dim[-1], x_dim)
self.output_activation = nn.Sigmoid()
def forward(self, x):
for layer in self.hidden:
x = F.relu(layer(x))
return self.output_activation(self.reconstruction(x))
class VariationalAutoencoder(nn.Module):
def __init__(self, dims):
super(VariationalAutoencoder, self).__init__()
[x_dim, z_dim, h_dim] = dims
self.z_dim = z_dim
self.flow = None
self.encoder = Encoder([x_dim, h_dim, z_dim])
self.decoder = Decoder([z_dim, list(reversed(h_dim)), x_dim])
self.kl_divergence = 0
for m in self.modules():
if isinstance(m, nn.Linear):
init.xavier_normal(m.weight.data)
if m.bias is not None:
m.bias.data.zero_()
def _kld(self, z, q_param, p_param=None):
(mu, log_var) = q_param
if self.flow is not None:
f_z, log_det_z = self.flow(z)
qz = log_gaussian(z, mu, log_var) - sum(log_det_z)
z = f_z
else:
qz = log_gaussian(z, mu, log_var)
if p_param is None:
pz = log_standard_gaussian(z)
else:
(mu, log_var) = p_param
pz = log_gaussian(z, mu, log_var)
kl = qz - pz
return kl
def add_flow(self, flow):
self.flow = flow
def forward(self, x, y=None):
z, z_mu, z_log_var = self.encoder(x)
self.kl_divergence = self._kld(z, (z_mu, z_log_var))
x_mu = self.decoder(z)
return x_mu
def sample(self, z):
return self.decoder(z)
应用
数据生成
指定$p(z)$为标准正态分布,将已经训练好的decoder与标准正态分布结合起来进行采样,生成与训练集相似的新样本。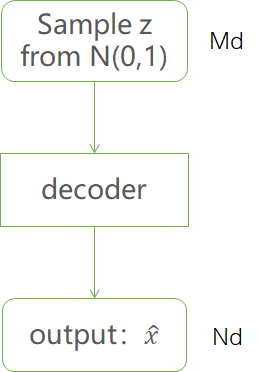
分别由CE和MSE损失训练的decoder进行采样生成的结果可视化:
高维数据可视化
encoder将数据$x$映射到低维$z$空间。
CE与MSE损失的可视化结果: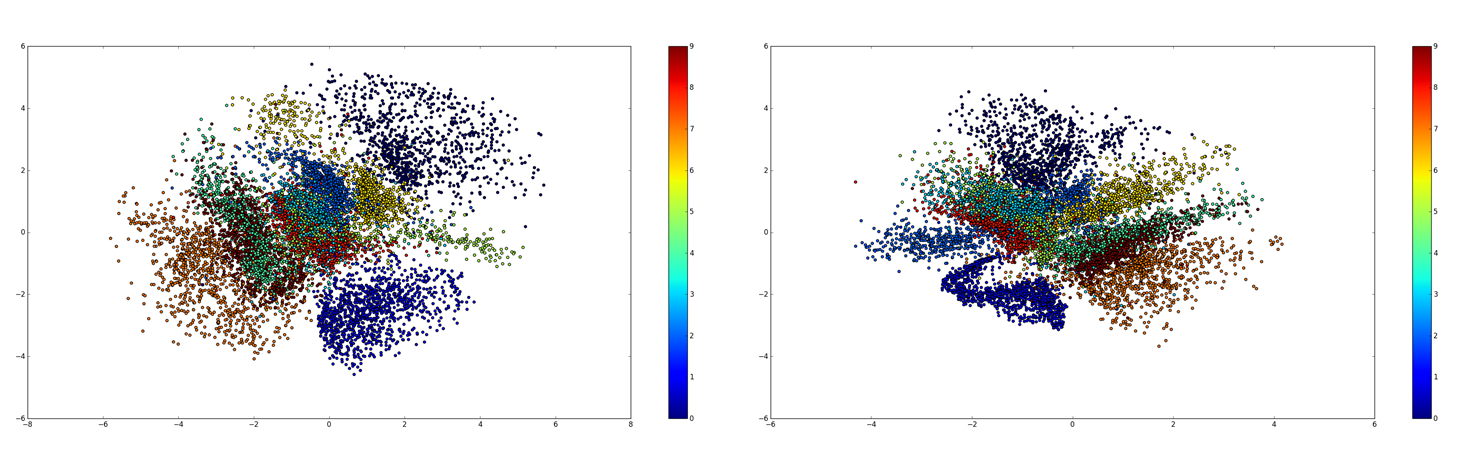
缺失数据填补(imputation)
很多实际问题中样本各维数据间存在相关性,在部分维度缺失或不准确时可以通过这一特性进行填补。

semi-supervised learning
半监督学习利用小部分带标注数据和大量无标注数据来学习预测模型,VAE学习到的特征可以用来作无监督。
指路Part2
reference:
https://blog.csdn.net/jackytintin/article/details/53641885

