RNN(Recurrent Neural Networks)

结构

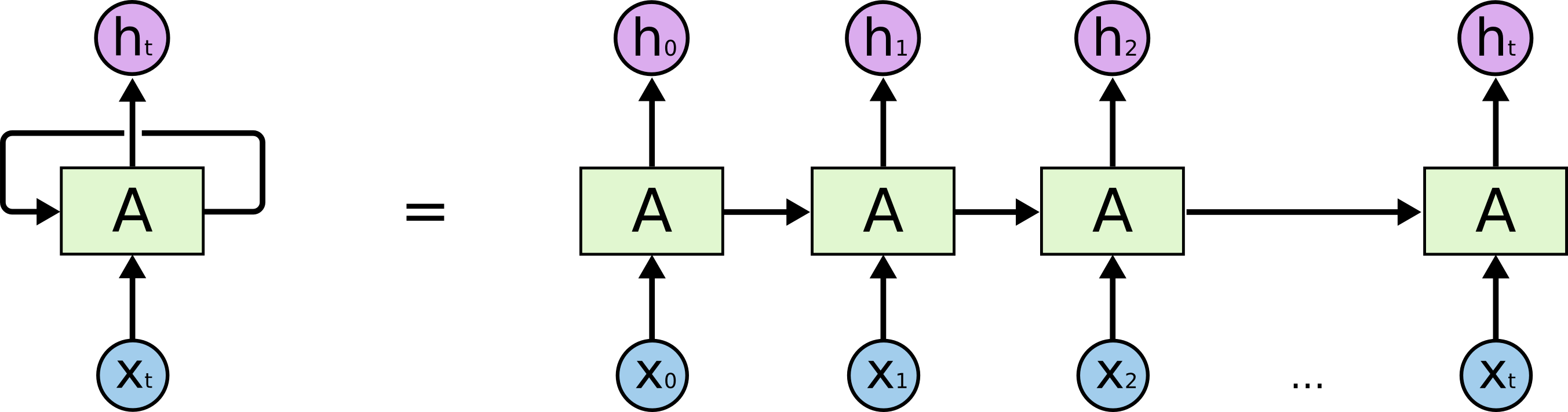
RNN包含循环，允许信息持久化

前向传播

$h^{(t)}$为隐藏状态，$L^{(t)}$为损失函数，$o^{(t)}$是模型输出，$\hat{y}^{(t)}$是真实输出。

t时刻的隐藏状态$h^{(t)}=\sigma(Ux^{(t)}+Wh^{(t-1)}+b)$, $\sigma$为激活函数，一般为tanh，也就是说当前的隐藏状态由输入和上一时刻的隐藏态决定。

$$o^{(t)}=Vh^{(t)}+c$$ $$y^{(t)}=\sigma(o^{(t)})$$

由于RNN是识别类的分类模型，激活函数为softmax。

反向传播

BPTT(back propagation through time)

模型参数$U, W, V, b ,c$在序列的各个位置共享，反向传播更新相同的参数

？什么是更新相同的参数……

就是说将每一时刻的梯度计算出来相加得到最终的梯度。

损失函数定义为对数损失函数，最终的损失函数$L=\sum_{t=1}^\tau L^{(t)}$

对数损失函数logstic loss function, log-likelihood loss function在logstic regression中使用

MLE(Maximum Likelihood Estimation)

$cost(\hat{y},y)=-y_i\log (\hat{y}))-(1-y_i)\log(1-\hat{y})$

针对二分类问题的表示，当y=1时，如果预测结果也为1则损失为0，如果预测为0则损失非常大，同理，y=0时一样

针对多分类问题，有NLLLoss(negative log likelihood loss), torch.nn.NLLLoss

$l=-\frac{\sum_{i=0}^{N-1} t_i\log y_i}{N}$

$t_i$是gt的one hot，y是网络输出

输入每一类概率的对数(logsoftmax)

fc + cross entropy loss = fc + logsoftmax + NLLLoss

$$\frac{\partial L}{\partial c} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial c} \\= \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial c} \\= \sum\limits_{t=1}^{\tau}\hat{y}^{(t)} - y^{(t)}$$

中间推导过程：

$$\frac{\partial o^{(t)}}{\partial c}=1$$ $$\frac{\partial L^{(t)}}{\partial o^{(t)}}=\frac{\partial L^{(t)}}{\partial \hat{y}^{(t)}}\frac{\partial \hat{y}^{(t)}}{\partial o^{(t)}}\\=\hat{y}^{(t)}-y^{(t)}$$

-log softmax求导：

$$\frac{\partial y}{\partial x_i}=-1 \text{if i is the right class, else }softmax(x_i)$$

cross entropy链式求导
https://blog.csdn.net/qian99/article/details/78046329

softmax求导：分为$i=j,i\neq j$两种情况

$$\frac{\partial a_j}{\partial z_j}=\frac{\partial}{\partial z_j}(\frac{e^{z_j}}{\sum_ke^{z_k}})\\=-\frac{e^{z_j}\sum_ke^{z_k}-e^{2z_j}}{(\sum_ke^{z_k})^2}\\=\frac{e^{z_j}}{\sum_ke^{z_k}}(1-\frac{e^{z_j}}{\sum_ke^{z_k}})\\=a_j(1-a_j)$$ $$\frac{\partial a_j}{\partial z_i}=\frac{\partial}{\partial z_i}(\frac{e^{z_j}}{\sum_ke^{z_k}})\\=-\frac{e^{z_j}}{(\sum_ke^{z_k})^2}e^{z_i}\\=-a_ia_j$$

cross entropy导数推导

定义$C=-\sum_iy_i\ln a_i, a_i=\frac{e^{z_i}}{\sum_ke^{z_k}}$

$\frac{\partial C}{\partial a_j}=\frac{\partial(-\sum_jy_j\ln a_j)}{\partial a_j}=-\sum_jy_j\frac{1}{a_j}$

最终合成的结果：

$$\frac{\partial C}{\partial z_i}=\frac{\partial C}{\partial a_j}\frac{\partial a_j}{\partial z_i}\\=-\sum_jy_j\frac{1}{a_j}\frac{\partial a_j}{\partial z_i}\\=-\frac{y_i}{a_i}a_i(1-a_i)+\sum_{j\neq i}\frac{y_j}{a_j}a_ia_j\\=-y_i+a_i\sum_ky_k$$

对于分类问题而言，y是one-hot,和为1，则最终结果为$-y_i+a_i$

$$\frac{\partial L}{\partial V} =\sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial V} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial V} = \sum\limits_{t=1}^{\tau}(\hat{y}^{(t)} - y^{(t)}) (h^{(t)})^T$$

$V$与$c$相比只是多了一项$h^{(t)}$

其余三个参数$W, V, b$的计算涉及到时序，比较复杂，定义序列索引$t$位置隐藏态梯度为$\delta^{(t)}=\frac{\partial L}{\partial h^{(t)}}$，然后从$\delta^{(t+1)}$递推$\delta^{(t)}$：

$$\delta^{(t)} =\frac{\partial L}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial h^{(t)}} + \frac{\partial L}{\partial h^{(t+1)}}\frac{\partial h^{(t+1)}}{\partial h^{(t)}} \\= V^T(\hat{y}^{(t)} - y^{(t)}) + W^T\delta^{(t+1)}diag(1-(h^{(t+1)})^2)$$

对于$\delta^{(\tau)}$，已经是最后一个索引序列：

$$\delta^{(\tau)} =\frac{\partial L}{\partial o^{(\tau)}} \frac{\partial o^{(\tau)}}{\partial h^{(\tau)}} = V^T(\hat{y}^{(\tau)} - y^{(\tau)})$$

tanh的导数:$f’(x)=1-f^2$

sigmoid的导数:
$f(x)=\frac{1}{1+e^{-z}},f’(x)=f(1-f)$

根据递推式计算出$\delta^{(t)}$后可以计算相对于$W, U, b$的导数：

$$\frac{\partial L}{\partial W} = \sum\limits_{t=1}^{\tau}\frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial W} \\= \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2)\delta^{(t)}(h^{(t-1)})^T$$ $$\frac{\partial L}{\partial b}= \sum\limits_{t=1}^{\tau}\frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial b} \\= \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2)\delta^{(t)}$$ $$\frac{\partial L}{\partial U} = \sum\limits_{t=1}^{\tau}\frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial U} \\= \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2)\delta^{(t)}(x^{(t)})^T$$

---

• ← Previous Post
• Next Post →